桥梁抗震3_Pushover
桥梁抗震3_Pushover
MidasCivil Pushover运用
Pushover的提出
因双柱墩在变化水平力作用下,两个墩轴力在不停变化,导致弯矩曲率曲线在不停变化。
Push-over算法是Freeman等人于1975年提出的。经过多年的研究发展,Push-over算法目前已被美国、日本、中国等国建筑抗震设计规范所接受,成为抗震结构弹塑性分析的主要方法之一。
Push-over算法的基本作法是:对结构逐级单调施加按某种方式模拟地震水平惯性力的水平侧向力并进行静力弹塑性分析,直至结构达到预定状态(成为机构、位移超限或达目标位移)。究其本质而言,Push-over 算法是静力分析方法。但与一般静力非线性分析方法不同之处在于其逐级单调施加的是模拟地震水平惯性力的侧向力。
Pushover算法的突出优点在于它既能考虑结构的弹塑性特性且工作量又较时程分析法大为减少。
Pushover基础模型介绍
不断增加盖梁中心节点的横向位移量,随着横向位移的增加,桥墩出现塑性铰,墩顶(底)的曲率增大。一旦曲率达到极限曲率(考虑安全系数2),此时墩顶盖梁中心的横向位移即为所求的位移值。
在推的过程中,由于极限曲率与轴力直接相关,或者说极限曲率是通过计算桥墩的M-PHI曲线得到的。在整个过程中轴力在不断变化,极限曲率也随之变化,故需要通过迭代的方法才能得到最终的允许位移值。首先假设恒载轴力,计算极限曲率。再从计算曲率中找到此曲率对应的步骤,从而查阅此步骤下的轴力值,用此轴力计算新的极限曲率,继续查阅新的步骤,直至某一步骤的轴力和曲率与M-PHI计算得到的曲率正好匹配停止迭代。
Pushover模型中需要定义边界条件与整体模型一致。支座传递上部荷载通过节点荷载施加,另外需要考虑桥墩自重影响。除此以外需要设置一个Pushover工况,此工况为施加在控制节点上的一个水平力(力的大小可任意指定,此例为100kN),用于确定推倒模式。
Midas操作
1. 建立单个桥墩模型
PS. 盖梁上恒载可以加至桥墩顶部,不必完全按支座加载,对结果影响不大。
2. 主控数据
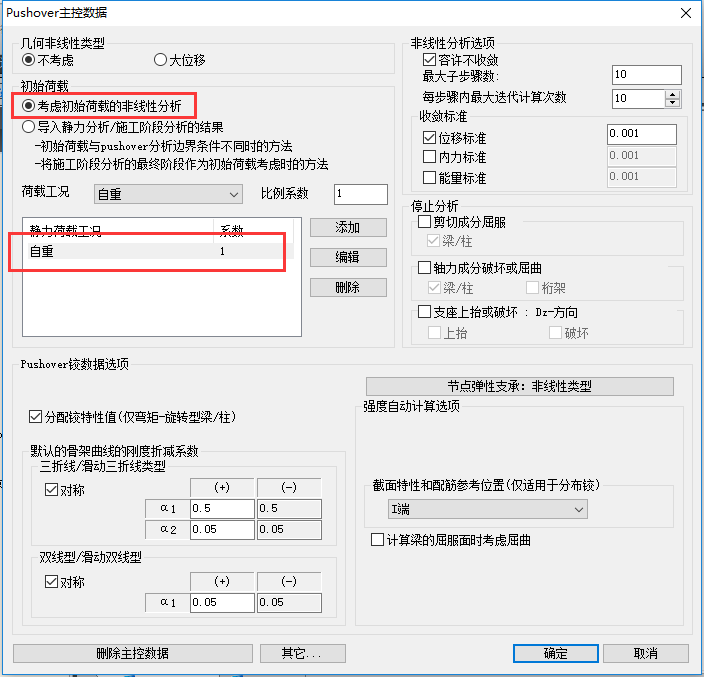
考虑初始的自重荷载
3. 荷载工况
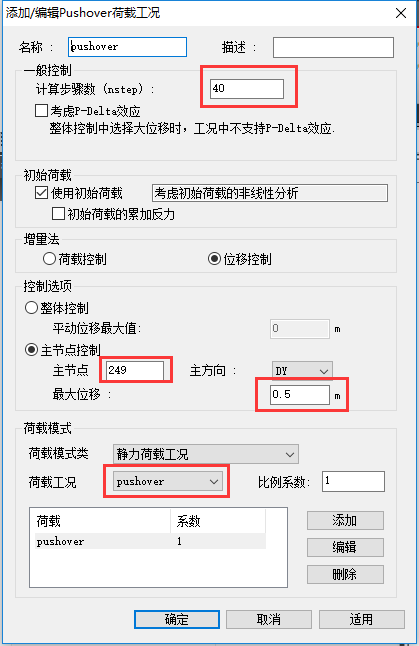
节点一般为盖梁顶节点
增量法:求剪力用荷载控制,求位移用位移控制。每次增量数值,荷载控制时就是设置的剪力/步骤数;位移控制时就是设置的最大位移/步骤数。
位移控制时,工况力的数值没有意义,仅方向有意义。
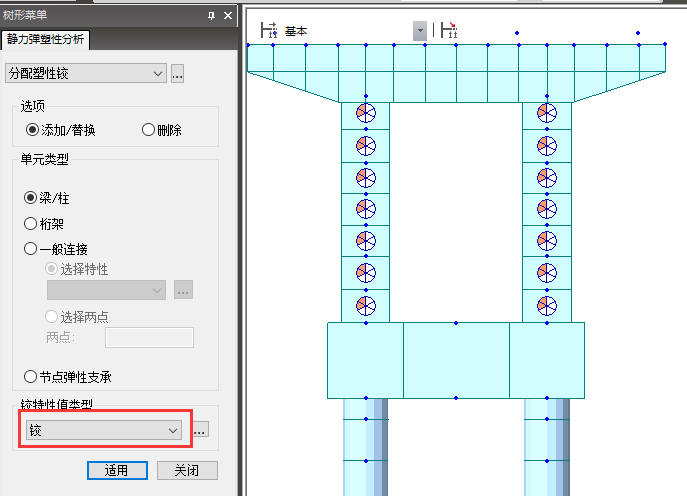
4. 定义Pushover铰特性值
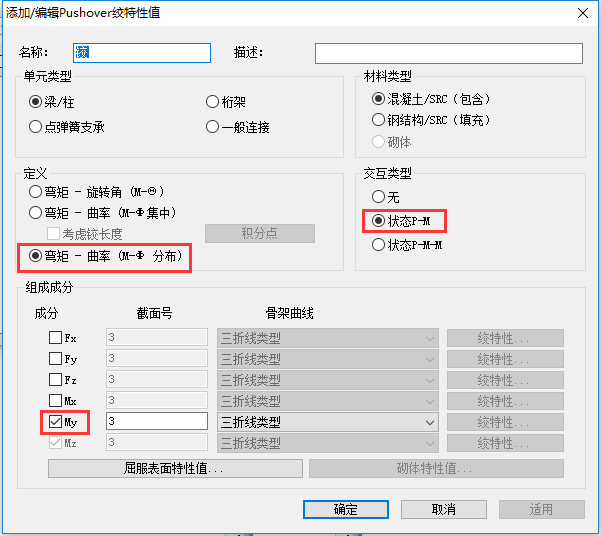
PS. Pushover的铰特性中,集中铰输出转角结果,分布铰输出曲率结果。交互类型中“无”需要用户自己定义弯矩和曲率的非线性关系,“P-M”是通过屈服面确定弯矩曲率的非线性关系,“P-M-M”是通过三轴屈服球确定非线性关系。对于混凝土结构“P-M-M”不适用。此处选择“P-M”,程序这里仅定义屈服面的定义规则,分配特性铰后,程序会根据这里的规则和程序的配筋情况计算最终的铰特性值。
绞特性值自带计算:
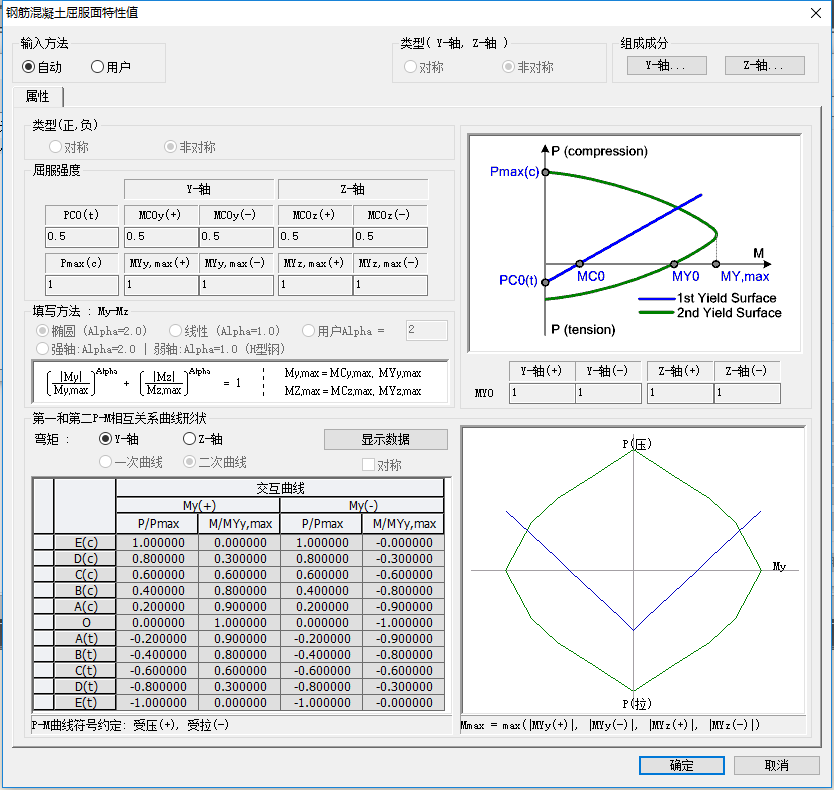
5. 分配Pushover铰特性值
6. 运行Pushover分析(全部)
7. 按需求运用
1)查看验算剪力时
- 查看恒载工况下极限弯矩,计算超强弯矩的剪力值,求得各墩剪力值之和。(抗规6.7.5)
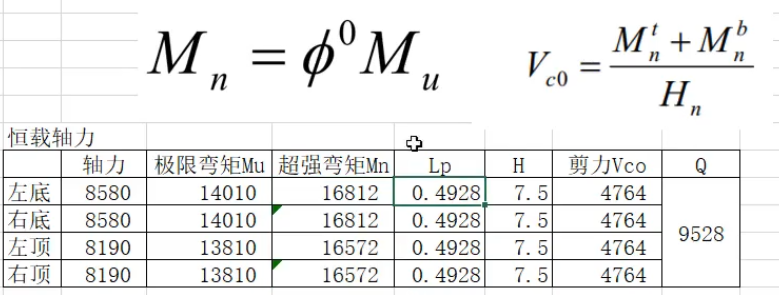
- 再由此剪力进行Pushover(第一次迭代),得到的墩顶剪力值和再进行Pushover(第n次pushover),直到两次计算的剪力和相差10%。
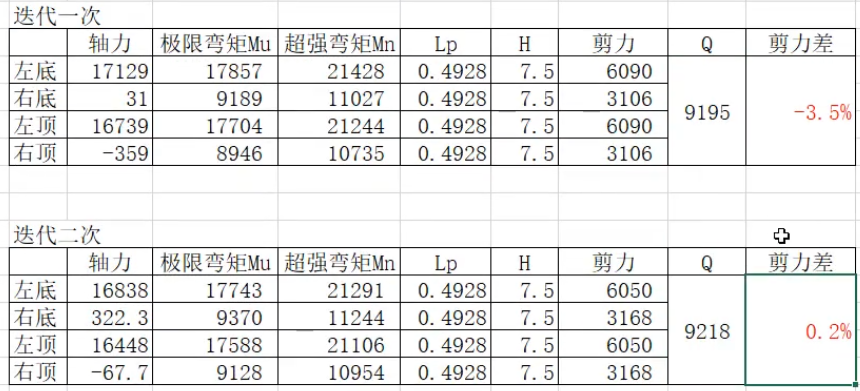
- 由此可得各墩柱轴力、超强弯矩、剪力设计值。
2)求解横向允许位移
根据恒载轴力计算的极限曲率在Pushover的步骤中查找相应曲率。
如果设定位移曲率最大值,小于恒载轴力下的曲率值,说明恒载轴力与极限位移对应步骤的轴力相差较大。将轴力假设为最后一个步骤的轴力值再次计算曲率。
由查到的相应步骤反查曲率、轴力、墩顶位移。并由上一个步骤的轴力值继续迭代,直至轴力差异较小,视为收敛(规范没有收敛标准),可认为在5%以内。

可知考虑延性安全系数2.0后的极限曲率。
由安全极限曲率,反查步骤的墩顶位移,即为容许位移。